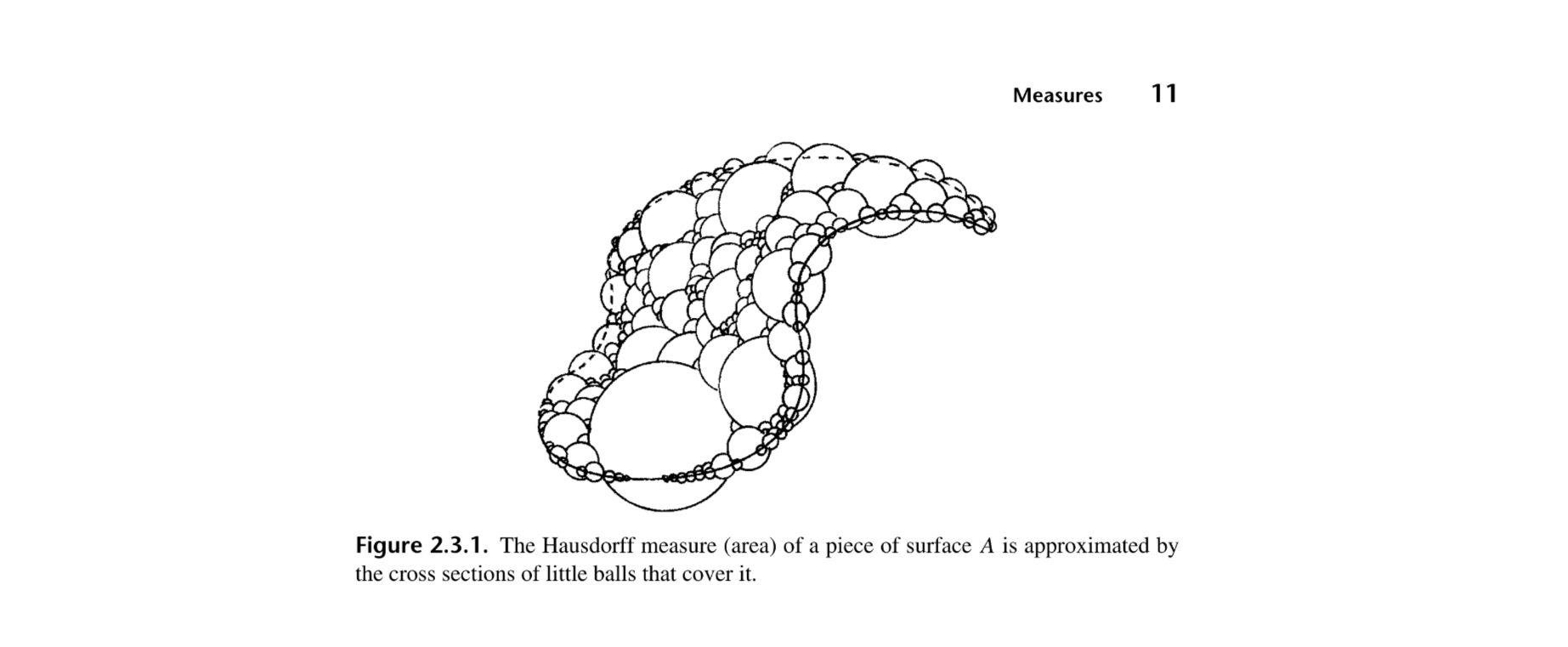
Medida de Hausdorff
Sejam s > 0 e \delta > 0. Definimos a medida exterior de Hausdorff s-dimensional em um espaço métrico M, refinada até \delta, como
para alguma constante \alpha(s) (geralmente, queremos que a medida de Hausdorff de uma bola coincida com a sua medida Lebesgue). Finalmente, definimos a medida de Hausdorff s-dimensional em si como o limite
Mensurabilidade de subconjuntos
Vimos em teoria geométrica de medidas que borelianos são mensuráveis para \Hmeas:
Cada \Hdmeas é uma medida exterior, e \Hmeas também é. Não só isso, mas \Hmeas são medidas Borel regulares.
Isso nos leva ao seguinte questionamento: quando as medidas \Hdmeas são Borel, e quando não são? Mostraremos o seguinte lema:
Se estamos em \RR^d e s < d, as medidas \Hdmeas nunca são Borel.
Isso segue da seguinte afirmação mais forte:
Se E \subseteq M for limitado1 e \delta > 0 forem tais que \Hdmeas(E) \neq \Hmeas(E), então E não é mensurável para \Hdmeas.
Sejam E e \delta como no enunciado.
A cada \delta-cobertura \mathcal{C} = \{ C_i \}_{i = 1}^{\infty} do conjunto E, chamaremos de diâmetro da cobertura \mathcal{C} o menor número \diam(\mathcal{C}) tal que \mathcal{C} é uma \diam(\mathcal{C})-cobertura. Mais explicitamente, \diam(\mathcal{C}) \coloneqq \sup \{ \diam(C_i) \mid i \in \NN \}. Seja também c(\mathcal{C}) = \alpha(s)\sum_{i = 1}^{\infty} \diam(C_i)^s o custo
da cobertura, de forma que \Hdmeas(E) = \inf_{\diam (\mathcal{C}) < \delta} c(\mathcal{C}).
Afirmamos que
Intuitivamente, isso quer dizer que as melhores aproximações de \Hdmeas(E) são por coberturas de diâmetro grande. De fato, de \ell > 0 segue que existe \varepsilon > 0 tal que toda cobertura \mathcal{C} de diâmetro \diam(\mathcal{C}) < \ell é tal que c(C) \geq \Hdmeas(E) + \varepsilon. Vamos usar isso mais adiante.
Para ver que a afirmação é verdade, suponha que fosse \ell = 0. Então existiriam coberturas (\mathcal{C}_i)_i com \diam (\mathcal{C}_i) \to 0 e c(\mathcal{C}_i) \to \Hdmeas(E). Mas como \Hdmeas[s][\diam(C_i)](E) \leq c(\mathcal{C}_i), temos
o que contradiz a hipótese.
Nesse ponto, já podemos mostrar que \Hdmeas não é Borel para todo \delta > 0 e s < d em \RR^d. De fato, se fosse Borel, tomando E = [0,1)^d, sabemos que \HD(E) = d, logo \Hmeas(E) = \infty, enquanto \Hdmeas(E) < \infty já que E é limitado. Pelo argumento acima, existem \ell > 0 e \varepsilon > 0 tais que se \mathcal{C} é uma \ell-cobertura de E, então c(\mathcal{C}) \geq \Hdmeas(E) + \varepsilon.
Agora, note que podemos dividir E em finitos borelianos disjuntos de diâmetro menor que \ell (por exemplo, fazendo interseções com pequenos cubos). Vamos chamar de (E_k)_{k = 1}^N essa partição de E em borelianos. Como cada E_k tem diâmetro menor que \ell, para cada k podemos escolher uma \ell-cobertura \mathcal{C}_k de E_k tal que c(\mathcal{C}_k) < \Hdmeas(E_k) + \varepsilon/N. Como estamos por hipótese supondo que \Hdmeas é borel, temos que \mathcal{C} = \bigcup_{k = 1}^N C_k é uma \ell-cobertura de E tal que
e chegamos em uma contradição.
A nota acima é interessante, pois mostra que basta dividirmos o conjunto E em pedaços mensuráveis de diâmetro suficientemente pequeno para chegarmos em uma contradição. Essa será a nossa tarefa no resto da demonstração, já que queremos mostrar que o conjunto E, em particular, é não-mensurável, e não podemos contar com a mensurabilidade dos cubos como fizemos para desprovar a propriedade Borel.
Para isso, vamos usar o seguinte teorema:
Se (\mathcal{B},\mu,M) é um espaço de medida finita não-atômico, então \mu(\mathcal{B}) = [0,\mu(M)].
Suponha que E é \Hdmeas-mensurável. Aplicaremos o teorema para medidas \mu_A = \Hdmeas|_A, onde A \subseteq E são mensuráveis. O primeiro fato a se notar é que \Hdmeas não pode ter átomos contidos em E — apenas nesse ponto usaremos a hipótese de E ser limitado, mas não sei se realmente é necessária. Como E é limitado, temos E \subseteq B onde B = B(0, \sup_{x \in E} d(0, x) + 1). Assim, se houvesse um átomo A \subseteq E, como \Hdmeas é invariante por translação, os conjuntos A_x = A + x\vec{e}_1 para x \in [-1,1] formariam um conjunto infinito de átomos, todos contidos em B, o que contradiz o fato de B ter medida \Hdmeas finita.
Agora, como estamos na hipótese do teorema e 0 < \Hdmeas(E) < \Hmeas(E) \leq \infty, podemos tomar A_1 \subseteq E mensurável com medida \Hdmeas(A_0) = \eta/2, onde \eta \coloneqq \min\{\Hdmeas(E),\alpha(s)\ell^{s}\}. Aplicando o teorema indutivamente, podemos tomar A_{i} \subseteq E \setminus \bigcup_{k = 1}^{i - 1}A_k tal que \Hdmeas(A_{i}) = \eta/2, desde que \Hdmeas\left(E \setminus \bigcup_{k = 1}^{i - 1} A_k\right) \geq \eta/2. Chamaremos de N o menor inteiro tal que \Hdmeas\left(E \setminus \bigcup_{k = 1}^{N - 1} A_k\right) < \eta/2, e definimos A_N = E \setminus \bigcup_{k = 1}^{N - 1} A_k. Assim, obtivemos uma partição \{ A_i \}_{i = 1}^N de E por conjuntos mensuráveis de medida menor que \eta/2.
Para cada 1 \leq i \leq N, seja \mathcal{C}_i = (C_{i,k})_{k \in \NN} uma cobertura de A_i tal que c(C_i) < \Hdmeas(A_i) + \min \{ \eta/2, \varepsilon/N \}. Note que \mathcal{C}_i são \ell-coberturas, pois
Isso significa que \mathcal{C} = \bigcup_{i = 1}^{N}\mathcal{C}_i é uma \ell-cobertura de E tal que
contradição.
-
não sei se realmente precisa que seja limitado
↩︎